Depth is the distance of a atom/residue to its closest molecule of bulk solvent.

Step 1: Solvating the Protein Molecule

The protein molecule of interest is placed at the center of a pre-equilibrated box of solvent (water). Full atomic water model SPC216 (generated using GROMACS [Hess et at, 2008] genbox with spc216.gro structural file) is used here.
The water molecules that clash with atoms of the protein (within 2.6Å of protein atoms) are removed from the box.

Step 2: Solvating the Protein Molecule

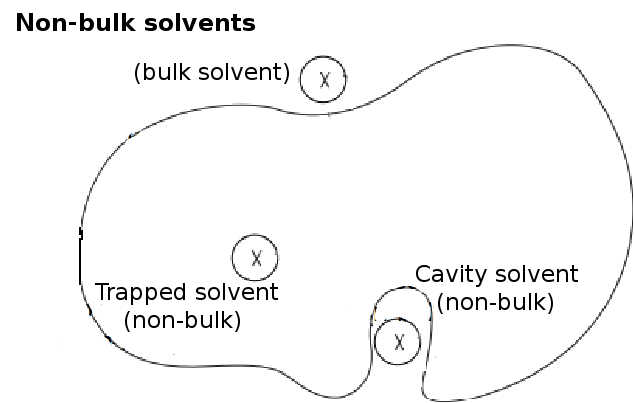
Other than the clashing water molecules, non-bulk waters are also removed from the box.

Non-bulk waters are those that are trapped in cavities (Figure 1) and isolated from the bulk solvent.

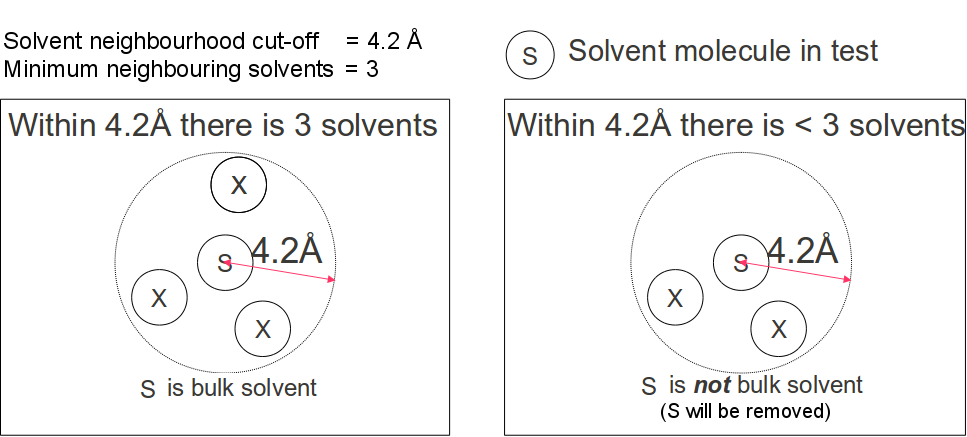
Isolated water are detected by inspecting the number of water molecules in its immediate neighborhood.

A water molecule is considered non-bulk if there are less than a specified minimum number of neighborhood waters (default value = 4) within a spherical volume of a specified solvent neighborhood radius(default value 4.2Å, Figure 2).
The removal of a cavity water causes its immediately neighboring waters to lose one neighborhood water molecule. For this reason, the check and removal of non-bulk waters is iterated until there is no further removal of water from the solvent box. For practical reasons, users are advised to vary the minimum number of neighborhood waters in the range 1 - 5. Checking for larger number of neighborhood waters often results in the removal of all water molecules.

Step 3: Sampling Solvent Configurations

The bulk water surrounding a protein is freely diffusing. To mimic this dynamics of bulk water, the protein is solvated repeatedly, each time in a different orientation. New orientations are generated by rotating the protein by a random angle about an axis passing through its center of mass, and translating it along the X-axis to a random distance < 2.8 Å (the average distance between neighboring water molecule in the box). Each solvation of the protein is considered to represent a snapshot of the dynamics of bulk-water. With sufficient number of solvations, water molecules can explore all regions accessible to bulk solvent, hence mimicking bulk-water dynamics (Figure 3).
At each solvation iteration, the value of atom/residue depth is computed as the distance between the atom/residue to the closest molecule of bulk water. Depth is finally reported as the average depth over all solvation iterations. The user can specify the 'number of solvation cycles '(default = 25).
Note: Run time scales linearly with number of solvation cycles.

Step 1: Constructing Binding Cavity Probability Tables for Amino-Acids

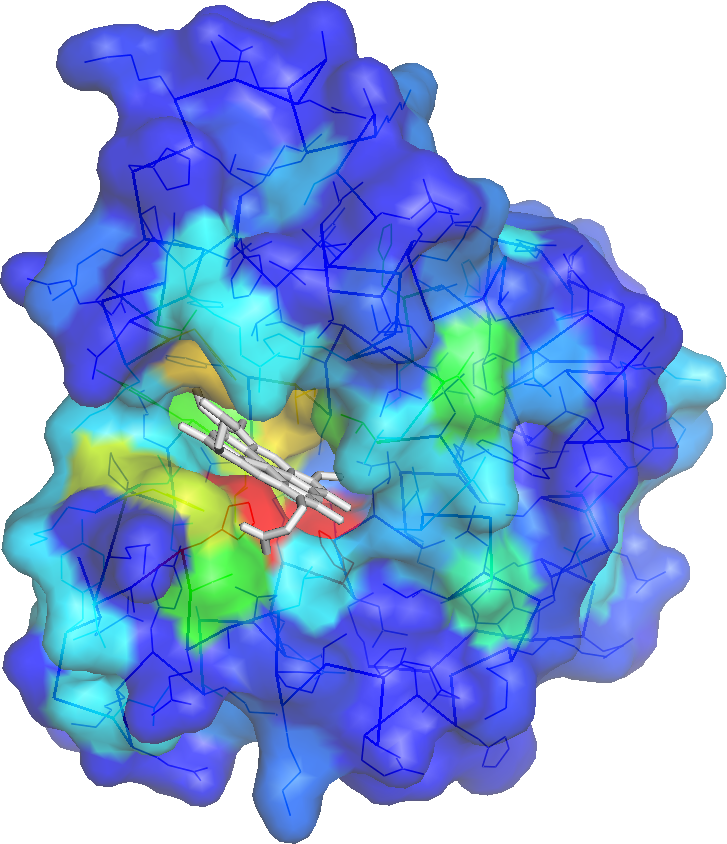
A binding cavity is a protein sub-structure of conserved geometrical and chemical properties complimentary to its bound ligand. Using a training-set of ligand bound high resolution crystal structures of proteins, residue depth and solvent-accessible area values were computed for all residues. The probability of individual amino acids to form part of the binding cavity is parametrized by the residue depth, accessible area value pairs (Figure 4)

Step 2: Assigning Probability Values onto Protein of Interest

For an query protein, solvent accessibility and depth are computed for all residues. Residues are assigned binding cavity probability values corresponding to solvent accessibility, residue depth value pairs. (Figure 5). If evolutionary information is used in making the predictions, 3 iterations of PSI-BLAST is used to create a multiple sequence alignment of homologues of the query (e-value cut-off of 0.00001). From this multiple sequence alignment a entropy value is computed and the probability value of the residues are then an average of the Depth/ASA prediction probability values and the entropy probability values.

Step 3:Grouping Cavity Residues

1. All residues with probability values above a user definable cavity prediction probability threshold are selected as binding cavity residues.
2. A 6.2Å sphere is built around each of these selected residue.
3. Starting from the residue with highest probability value, all other selected residues within this sphere are merged into the same binding cavity.
4. The process is repeated until no further merger occurs.
5. Finally, a 3.6Å sphere is built around every residue within each cavity.
6. All solvent-accessible residue (side-chain accessibility > 30%) that are a part of these spheres are also grouped into the binding cavities.

pKa is a measure of acidic strength and is defined as the logarithm of the acid dissociation constant. pKa of protein residues estimates the protonation strength of its ionizable groups. Ionizable residues play a significant role in several protein functions including folding, stability, solubility, protein-protein interactions etc. To gain insight into these function, it is often crucial to accurately determine the pKa of ionizable residues. The pKa values of ionizable groups are however highly sensitive to their enviroment. This sensitivity makes pKa estimation difficult. Here we introduce a simple method for pKa prediction. pKa predictions are made for the following ionizable residues: ASP, GLU, HIS and LYS residues using the formula: \begin{equation} \begin{array}{c} p K a_{\text {predicted }}=p K a_{\text {model }}+a_{1} * M C_{\text {depth }}+a_{2} * \text { polarSC }_{\text {depth }}+a_{3} *(\text { no.donors })+a_{4} *(\text { no. of acceptors }) \\ +a_{5} *(\text { elec })+a_{6} *\left(A S A_{\text {SC }}\right) \end{array} \end{equation}

where the predicted pKa is a correction to the model pKa. The model pKa for a particular amino acid residue is determined for the case when the titratable group is completely accessible to the solvent and minimally pertubed by the surrounding environment. The correction terms are in the form of a linear combination of 6 different features including main chain depth (MC_depth), polar side chain depth (polarSC_depth), number of H-bonds donors and acceptors (no. Hbonds_N and no. Hbonds_O), the electrostatic potential centred at the titratable group considering all partial charges within a cut-off distance of 8Å (elec) and the solvent accessible area of the side chain (ASA_SC) .

Aim

The server attempts to identify a small set of amino acid residues in a query protein that have a high probability of being buried (side-chain accessibilities less than 5%, expressed in terms of residue depth). The server suggests substitutions at these buried positions that are most likely to result in a temperature sensitive (Ts) phenotype.

Prediction Principles

The Ts phenotype has been shown to correlate with decreased protein stability and reduced levels of the protein, in vivo.

It has also been shown that substitutions of buried hydrophobic residues often result in significant destabilization of the protein, often much larger changes in protein stability than mutations at surface positions. Hence, our approach to predict substutions that result in a Temperature-sensitive mutant is to predict positions of hydrophobic residues in the protein that are likely to be buried.

Several cases of substitution of buried residue positions have been shown to result in a Ts phenotype,for example in the case of T4 lysozyme, and gene V protein.

Methods

Hydrophobicity Rescaling

The Rose Hydrophobicity scale is chosen to quantify the hydrophobicity of amino acid residues, as it most closely correlates with the degree of residue burial. In this study, the hydrophobicity values of the scale were chosen to be equal to the average extent of burial of the residue in the training set, i.e.

\[B_{i}=\left(A_{o i}-A_{i}\right) / A_{o i} \cdot 100 \%\]

Hydrophobic Residues

7 types of amino acid residues with rescaled hydrophobicity greater than 80, namely Cys, Phe, Ile, Val, Trp, Met, and Leu are defined as hydrophobic residues in this study. As Cys could be involved in disulfide bonds or metal ion coordination, they are not included in the prediction candidates.

Predicting Residue Burial

Burial is quantified using two parameters: 1) average hydrophobicity and 2) Hydrophobic moment.

Average Hydrophobicity of a residue (averaged over a seven residue window) is given by:

\[H_{a v}(j)=\sum_{n-j-3}^{j+3} H(n) / 7\]

where the H(n)s are the rescaled individual residue hydrophobicities listed above.

The hydrophobic moment, H_mom is calculated over a nine residue window as follows:

\[H_{m o m}(j)=\left\{\left[\sum_{n-j-4}^{j+4} H(n) \sin (\delta \cdot n)\right]^{2}+\left[\sum_{n-j-4}^{n+4} H(n) \cos (\delta \cdot n)\right]^{2}\right\}^{1 / 2}\]

where δ is the phase angle and is dependent on the periodicity of the secondary structure that the sequence is assumed to adopt:

• δ(Α-helix) = 100°.
• δ(flat β-sheet) = 180°
• δ(curved β-sheet) = 160°

Hydrophobic moment is introduced because both helices and β strands often have one solvent exposed hydrophilic face and one buried hydrophobic face. Buried regions of such sequences therefore cannot be identified using only H_av. In contrast, they can be indentified by average H_av and high H_mom values.

Prediction Criteria

The following prediction rules were generated by large scale analysis of data ( Varadarajan et al, 1996).

Substituition Table

The free energies of unfolding of typical globular proteins are in the range of 5 - 15 kcal/mol at room temperature. A Ts mutation should destabilize the protein by an amount that is an appreciable fraction of the free energy of folding at the nonpermissive temperature.

The exact amount of destabilization produced by a mutation will depend on the effect of the mutation on ΔG, ΔH, and ΔC_p. In general, these will not be known for the protein of interest. It is therefore desirable to make both conservative and nonconservative substitutions at predicted buried sites, so that at least one of these will result in a Ts phenotype.

Our approach is therefore to suggest five different substitutions at each predicted buried site that differ in the stereochemistry and polarity of the substituted residue. These substitutions span a wide range of free energy and, we assume that at least one of these substitutions would destabilize the protein to an extent appropriate for a Ts phenotype.